Introdução à Análise de Algoritmos
A análise de desempenho é uma etapa fundamental na concepção de um algoritmo. Diante de um problema computacional, diversas soluções podem ser propostas. Por exemplo, para ordenar um sequência de números, o desenvolvedor pode utilizar algoritmos como o BubbleSort, MergeSort, QuickSort entre outros. Entender como esses algoritmos se comportam à medida que aumentamos o tamanho da entrada a ser ordenada é primordial para decidirmos qual solução adotar em um determinado contexto.
Analisar um algoritmo significa prever a quantidade de recursos que tal algoritmo consome ao ser executado. A análise pode apontar diversos candidatos e, tipicamente, exclui diversas soluções não eficientes. Diversas variáveis podem ser objetos de estudo da análise de um algoritmo, por exemplo, consumo de memória, largura de banda de comunicação, entre outros. No entanto, com frequência, desejamos medir o tempo execução. E é essa variável que estamos interessados em discutir neste documento.
Uma abordagem direta para analisar o desempenho de um algoritmo é a abordagem empírica. Neste caso, configura-se um ambiente em que as variáveis são controladas e executa-se os algoritmos com o intuito de medir o tempo de computação e comparar as diferentes soluções. O tempo de execução (eixo y) é medido em função do tamanho da entrada (eixo x). Por exemplo, para analisar empiricamente um algoritmo de ordenação medimos o tempo de execução para diferentes tamanhos de arrays. Além disso, podemos querer variar a configuração do array sob ordenação para entender, por exemplo, como o algoritmo se comporta com um array já ordenado ou como se comporta com arrays parcialmente ordenados.
Tipicamente, executa-se um experimento com o tamanho da amostra suficiente para se ter validade estatística e permitir a construção de um modelo que represente a curva de cada algoritmo. A Figura abaixo apresenta os tempos de computação de diferentes algoritmos de ordenação à medida que aumenta-se o tamanho da entrada. Como podemos notar, o algoritmo SelectionSort apresenta tempo de execução consideravelmente maior em comparação com as outras três alternativas à medida que a quantidade de elementos a serem ordenados cresce.
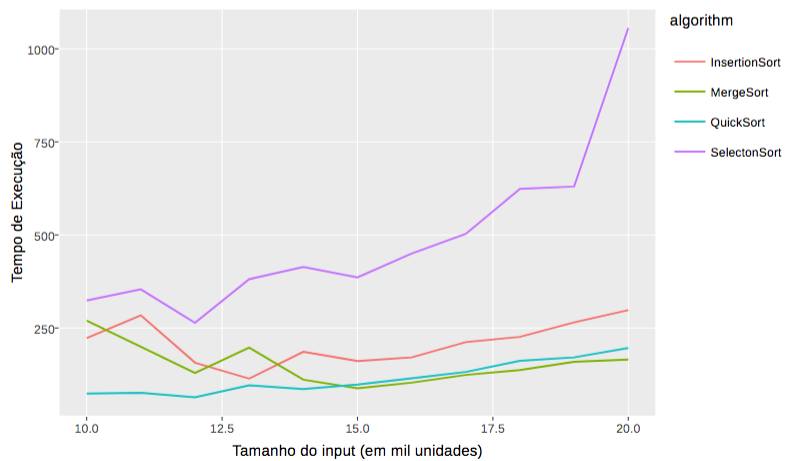
A abordagem empírica para análise de algoritmos é útil, pois, se conduzida de maneira metodologicamente apropriada, fornece valores precisos sobre o tempo de execução de um algoritmo. No entanto, essa abordagem apresenta algumas desvantagens. Primeiro, existe um alto custo relacionado à implementação de todos os algoritmos, além da configuração, execução e análise do experimento. Além disso, note que as conclusões são limitadas ao espaço de entrada do experimento. Por fim, os resultados são dependentes do hardware utilizado.
Diante do cenário exposto acima, surge a necessidade de uma análise que:
- seja independente de hardware;
- permita analisar os algoritmos em um espectro maior de entradas;
- seja simples.
Note que, em diversas situações, o interesse está em comparar algoritmos, ao invés de determinar o seu tempo exato de execução. Em particular, estamos interessados nas funções no comportamento dos algoritmos para grandes tamanhos de entrada – análise assintótica.
Análise de Algoritmos
Antes de apresentar os conceitos de análise assintótica, sua notação e modus operandi, é preciso apresentar a hipótese em que a análise de algoritmos se baseia:
Hipótese: O custo de operações primitivas é constante.
Essa hipótese estabelece que operações aritméticas, indexação de elementos em um vetor, retorno de métodos, atribuição de valores às variáveis, comparação de elementos, entre outros, executam em tempo constante, referenciado como $O(1)$ ou $O(C)$. É importante destacar que, na prática, esse custo varia de acordo com o hardware, linguagem de programação etc. No entanto, essa variação é insignificante do ponto de vista da análise assintótica. O quadro abaixo lista as operações primitivas detalhadamente.
Operações Primitivas * Avaliação de expressões booleanas (i >= 2; i == 2, etc); * Operações matemáticas (*, -, +, %, etc); * Retorno de métodos (return x;); * Atribuição (i = 2); * Acesso à variáveis e posições arbitrárias de um array (v[i]).
Nesse contexto, o tempo de execução de um algoritmo é a soma do custo das operações primitivas. Por exemplo, considere o algoritmo que multiplica o resto da divisão de dois inteiros pela parte inteira da mesma divisão:
int multiplicaRestoPorParteInteira(int i, int j) {
int resto = i % j;
int pInteira = i / j;
int resultado = resto * pInteira;
return resultado;
}
Passo 1: Identificar primitivas. O primeiro passo para determinar de modo analítico o tempo de execução de qualquer algoritmo é identificar todas as operações primitivas. Cada uma, como discutido anteriormente, tem um custo constante. Para o algoritmo acima temos:
-
atribuição (resto = ) -> $c_1$
-
operação aritmética (i % j) -> $c_2$
-
atribuição (pInteira = ) -> $c_3$
-
operação aritmética (i / j) -> $c_4$
-
atribuição (resultado = ) -> $c_5$
-
operação aritmética (resto * pInteira) -> $c_6$
-
retorno de método (return resultado) -> $c_7$
Passo 2: Identificar a quantidade de vezes que cada uma das primitivas é executada. Para o algoritmo acima, todas as primitivas são executadas apenas uma vez.
Passo 3: Somar o custo total. O tempo de execução do algoritmo é a soma das execuções das operações primitivas. Nesse caso temos que a função que descreve o tempo de execução é:
$f(n) = c_1+c_2+c_3+c_4+c_5+c_6+c_7$
Lembrando estamos interessados em uma função que nos diga o tempo de execução em relação ao tamanho da entrada. Nesse caso, escolhemos $n$ para representar o tamanho da entrada. Como pode ser visto na função detalhada, o custo não depende de $n$ de maneira alguma. Independente dos números passados como parâmetro, o custo será sempre o mesmo. Por isso dizemos que essa função, e portanto o algoritmo que é descrito por ela, tem custo constante, ou seja, independe do tamanho da entrada.
Dizer que um algoritmo tem custo constante significa dizer que o seu tempo de execução independe do tamanho da entrada.
Outro fator de destaque é que podemos considerar que todas as constantes possuem o mesmo valor $c$. Assim, podemos simplificar a função para $f(n)= 7c$.
E quando houver condicionais?
O uso de comandos condicionais é muito comum em nossos algoritmos e nos impõe uma dificuldade na análise do tempo de execução. Essa dificuldade está relacionada ao fato de que, dependendo do caso, apenas uma parte do código é executada. Como decidir como fazer a análise? Que caminho devemos computar?
Nesse caso, escolhemos o pior caso. Neste curso estamos interessados em saber como os algoritmos se comportam no seu pior caso. Essa análise nos dá uma visão muito clara sobre o que posso esperar da execução de um algoritmo. Por exemplo, se você me disser que seu algoritmo de ordenação termina a execução em no máximo 3 segundos para uma determinada entrada, eu tenho uma ideia clara sobre o que posso esperar. No entanto, se você me disser que o algoritmo termina a execução em 3 segundos ou mais, eu não tenho muita certeza sobre o que esse “mais” significa. Pode significar 5 segundos, 50 segundos, 5 anos…
A análise de pior caso é, portanto, útil para eliminarmos soluções ruins. Além disso, o melhor caso raramente acontece, ao contrário dos outros casos que podem ser bem mais comuns. Por último, o caso médio, além de demandar análise estatística, muitas vezes é muito semelhante ao pior caso.
Para demonstrar a análise de pior caso, vamos analisar um método que recebe as três notas de um aluno e calcula a nota que ele precisa obter na prova final, se esse for o caso. Se o aluno for aprovado ($media >= 7.0$) ou reprovado sem direito a final ($media < 4$), o método deve retornar $0$.
double precisaNaFinal(double nota1, double nota2, double nota3) {
double media = (nota1 + nota2 + nota3) / 3;
if (media >= 7 || media < 4) {
return 0;
} else {
double mediaFinal = 5;
double pesoFinal = 0.4;
double pesoMedia = 0.6;
double precisa = (mediaFinal - pesoMedia * media) / pesoFinal;
return precisa;
}
}
Passo 1. Identificar primitivas.
-
atribuição (media = ) -> $c_1$
-
operação aritmética (nota1 + nota2 + nota3) -> $c_2$
-
operação aritmética (… / 3) -> $c_3$
-
avaliação de expressão booleana (media >=7 || media < 4) -> $c_4$
-
retorno de método (return 0) -> $c_5$
-
atribuição (mediaFinal = ) -> $c_6$
-
atribuição (pesoFinal = ) -> $c_7$
-
atribuição (pesoMedia = ) -> $c_8$
-
atribuição (precisa = ) -> $c_9$
-
operação aritmética (pesoMedia * media) -> $c_{10}$
-
operação aritmética (mediaFinal - …) -> $c_{11}$
-
operação aritmética (… / pesoFinal) -> $c_{12}$
-
retorno de método (return precisa) -> $c_{13}$
Passo 2: Identificar a quantidade de vezes que cada uma das primitivas é executada. Aqui vem a grande diferença. Como estamos interessados no pior caso, nós vamos descartar a constante $c_5$, pois, no pior caso, o bloco do else será executado, uma vez que é mais custoso que o bloco do if. As outras primitivas são executadas apenas uma vez.
Passo 3: Somar o custo total.
$f(n) = c_1+c_2+c_3+c_4+c_6+c_7+c_8+c_9+c_{10}+c_{11}+c_{12}+c_{13}$
Note que $c_5$ é desconsiderada.
E quando houver iteração?
Nos dois exemplos que vimos até aqui todas as primitivas são executadas apenas uma vez e, por isso, o tempo de execução do algoritmo é sempre constante. Vejamos o que acontece quando há iteração. O código abaixo procura por um elemento em um array.
public static boolean contains(int[] v, int n) {
for (int i = 0; i < v.length; i++)
if (v[i] == n)
return true;
return false;
}
Passo 1: Identificar primitivas.
-
Atribuição (int i = 0) -> $c_1$
-
Avaliação de expressão booleana (i < v.length) -> $c_2$
-
Operação aritmética (i++) -> $c_3$
-
Avaliação de expressão booleana (v[i] == n) -> $c_4$
-
Retorno de método (return true) -> $c_5$
-
Retorno de método (return false) -> $c_6$
Observação Importante. Se lançarmos um olhar mais detalhista em algumas expressões, na verdade, vamos perceber que estamos passando por cima de algumas primitivas. Por exemplo, nesse exemplo nós consideramos que a expressão booleana v[i] == n é uma primitiva (c4), mas ela envolve também o acesso à v[i] e o acesso a n que, como sabemos, são também primitivas. Então, sendo bem detalhistas, teríamos que identificar 3 primitivas na expressão v[i] == n. Da mesma forma, a expressão i + j pode ser considerada como sendo 3 primitivas, isto é, o acesso à variável i, o acesso à variável j e a expressão aritmética. Eu escolhi não fazer isso por fins didáticos. Iríamos poluir muito nossa análise. Por isso, quando houver uma expressão booleana, mesmo que ela envolva outras primitivas, vamos considerar como apenas uma, ok? O mesmo será feito para expressões aritméticas.
Passo 2: Identificar a quantidade de vezes que cada uma das primitivas é executada.
Aqui mora a grande diferença da análise deste exemplo em relação aos demais. Em primeiro lugar, nem todas as primitivas são executadas apenas uma vez. Depois, temos que voltar a lembrar que estamos tratando do pior caso. Esse cenário é representado por um array que não contém o número procurado, pois o algoritmo irá realizar todas as iterações e retornar false no final. Veja que se o número procurado estiver presente, a execução pode terminar bem antes do fim da iteração no array. Isso significa que na nossa análise vamos descartar a primitiva $c_5$, pois no pior caso ela nunca é executada.
Dado que o tamanho do vetor (v.length) é $n$, temos:
-
$c_1$ é executada apenas uma vez.
-
$c_2$ é executada $(n+1)$ vezes. Exemplo: se $n = 5$, temos as seguintes verificações: 0 < 5, 1 < 5; 2 < 5, 3 < 5, 4 < 5 e 5 < 5, quando encerra-se o loop. Ou seja, 6 verificações.
-
$c_3$ é executada $n$ vezes. Exemplo: se $n = 5$, temos os seguintes incrementos em i: 1, 2, 3, 4 e 5, quando encerra-se o loop.
-
$c_4$ é executada $n$ vezes.
-
No pior caso, $c_5$ não é executada.
-
$c_6$ é executada apenas uma vez.
Passo 3: Somar o custo total.
O tempo de execução do algoritmo é a soma das execuções das operações primitivas. Nesse caso temos que a função que descreve o tempo de execução é:
$f(n) = c_1+c_2*(n+1)+c_3*n+c_4*n+c_6$
Considerando todas as primitivas com custo $c$ e simplificando a função, temos:
$f(n) = 3*c*n+3*c$
Veja que essa função é diretamente relacionada ao tamanho do array ($n$). À medida que cresce o tamanho de $n$, cresce também o tempo de execução do pior caso. Esse crescimento é linear, pois a função é linear. Faz sentido, certo? Iterar em um array com 100 posições é 10 vezes mais lento que iterar em um array de 10 posições. Não é por acaso que o nome desse algoritmo é busca linear. O termo refere-se a ambos: i) a estratégia de procurar o elemento de modo sequencial em uma coleção e ii) o tempo de execução do algoritmo.
E quando houver loops aninhados?
public boolean contemDuplicacao(int[] v) {
for (int i = 0; i < v.length; i++)
for (int j = i + 1; j < v.length; j++)
if (v[i] == v[j])
return true;
return false;
}
Passo 1: Identificar primitivas.
-
Atribuição (int i = 0) -> $c_1$
-
Avaliação de expressão booleana (i < v.length) -> $c_2$
-
Operação aritmética (i++) -> $c_3$
-
Atribuição (int j = …) -> $c_4$
-
Operação aritmética (… = i + 1) -> $c_5$
-
Avaliação de expressão booleana (j < v.length) -> $c_6$
-
Operação aritmética (j++) -> $c_7$
-
Avaliação de expressão booleana (v[i] == v[j]) -> $c_8$
-
Retorno de método (return true) -> $c_9$
-
Retorno de método (return false) -> $c_{10}$
Passo 2: Identificar a quantidade de vezes que cada uma das primitivas é executada.
O pior caso de execução desse algoritmo é quando não há repetição de valores no array. Ou seja, os loops são executados até o final. Então, como estamos falando do pior caso, descartamos $c_8$, porque no pior caso essa primitiva nunca será executada.
Dado que o tamanho do vetor (v.length) é $n$, temos:
-
$c_1$ é executada apenas uma vez.
-
$c_2$ é executada $(n+1)$ vezes. Exemplo: se $n = 5$, temos as seguintes verificações: 0 < 5, 1 < 5; 2 < 5, 3 < 5, 4 < 5 e 5 < 5, quando encerra-se o loop. Ou seja, 6 verificações.
-
$c_3$ é executada $n$ vezes. Exemplo: se $n = 5$, temos os seguintes incrementos em i: 1, 2, 3, 4 e 5, quando encerra-se o loop.
Agora, atenção, porque vamos tratar das primitivas do laço mais interno.
-
$c_4$ e $c_5$ são executadas $n$ vezes. Serão executadas uma vez para cada loop interno. Exemplo: se $n = 5$, temos i = 0 e j = 0 + 1 = 1, i = 1 e j = 1 + 1 = 2, i = 2 e j = 2 + 1 = 3, i = 3 e j = 3 + 1 = 4, i = 4 e j = 4 + 1 = 5, quando i = 5 o laço interno não é executado.
-
A quantidade de execuções de $c_6$ depende do laço mais externo, pois $j$ varia de acordo com $i$ ($j = i+1$). Como o laço externo executa $n$ vezes, a quantidade de vezes que $j$ varia é dada por: $n + (n - 1) + (n - 2) + (n - 3) + (n-4) + …1$. Essa série representa uma Progressão Aritmética finita decrescente com razão 1. A soma de uma PA com essas características é dada por $S = n/2 * (a_1+a_n)$, onde $a_1$ e $a_n$ são o primeiro e o último elemento da sequência, respectivamente. Assim, para $a1=1$ e $an = n$, temos que $c_6$ é executada $({n^2 + n})/{2}$ vezes.
-
Como $c_7$ é executada uma vez a menos que $c_6$, então temos que o primeiro termo da PA é $a1 = 1$, $an = n - 1$ e $n = n - 1$. Assim, temos que $c_7$ é executada ${(n^2 - n)}/{2}$.
-
$c_8$ é executada a mesma quantidade de vezes que $c_7$.
-
$c_9$ não é executada nenhuma vez porque estamos falando do pior caso.
-
$c_{10}$ é executada apenas uma vez.
Passo 3: Somar o custo total.
O tempo de execução do algoritmo é a soma das execuções das operações primitivas. Nesse caso temos que a função que descreve o tempo de execução é:
$f(n) = c_1 + c_2*(n+1) + c_3 * n + c_4 * n + $
$c_5 * n + c_6 * (n^2 + n)/{2} + $
$c_7 * {(n^2 - n)}/{2} + c_8 * {n^2}/{2} + c_{10}$
Veja que essa função é diretamente relacionada ao tamanho do array (n). À medida que cresce o tamanho de $n$, cresce também o tempo de execução do pior caso. O tempo de execução do algoritmo cresce de forma quadrática em relação ao tamanho da entrada, pois a função é quadrática. Faz sentido, certo? Comparar cada elemento de um array com todos os outros é da ordem de $n^2$.
É importante que você entenda que esse algoritmo é bem mais lento do que o anterior, pois uma função quadrática cresce mais rapidamente que uma função linear.
No material sobre Análise Assintótica vamos aprender que essa função complicada pode ser simplificada para $n^2$ quando tratamos de grandes entradas, pois as constantes e os expoentes de menor magnitude não impactam muito nesse cenário.
Resumo
-
Calcular o tempo de execução de um algoritmo é muito importante.
-
Uma forma de calcular o tempo de execução é seguir os passos:
-
Identificar primitivas
-
Identificar o número de vezes que cada uma das primitivas é executada
-
Somar o custo total
-
-
É preciso estar atento para o fato de que estamos falando de análise do pior caso e, por isso, descartamos os fluxos alternativos de menor custo.