Árvores Balanceadas (AVL)
Contextualização
Árvores binárias são estruturas de dados fundamentais no contexto de Ciência da Computação. Em particular, Árvores Binárias de Pesquisa são aplicadas na solução de diversos problemas que demandam eficiência em operações básicas, como busca. Informalmente, uma Árvore Binária de Pesquisa (BST) é uma estrutura de dados de árvore binária baseada em nós, onde todos os nós da subárvore esquerda possuem um valor numérico inferior ao nó raiz e todos os nós da subárvore direita possuem um valor superior ao nó raiz. Formalmente, uma BST é definida recursivamente da seguinte forma:
- $A$ é uma árvore nula
- $A = (E, raiz, D)$ onde E e D são árvores binárias de pesquisa. $E$ contém apenas valores menores do que o armazenado na raiz, enquanto $D$ contém apenas valores maiores do que o armazenado na raiz
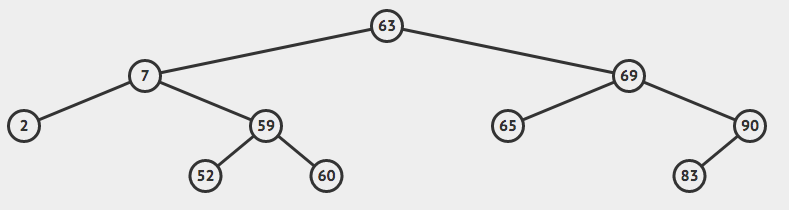
Um conceito bastante importante em BST é a altura. Altura de uma BST é definida pelo maior caminho entre a raiz e todas as folhas. No exemplo acima, a altura da raiz é 3. Esse conceito é importante pois várias operações básicas, como inserção, busca e remoção em uma BST são, do ponto de vista assintótico $O(h)$. Portanto, idealmente, é preciso manter h com o menor valor possível para que as operações sejam eficientes. No entanto, isso nem sempre é possível. Uma combinação de inserções e remoções pode levar a árvore a um estado em que a altura da sub-árvore à direita pode ser muito maior que a altura da sub-árvore à esquerda (e vice-versa). Quando a árvore atinge esse estado, dizemos que ela está desbalanceada.
O Problema
A figura abaixo mostra a adição dos elementos [1, 2, 3, 4, 5] em uma BST.
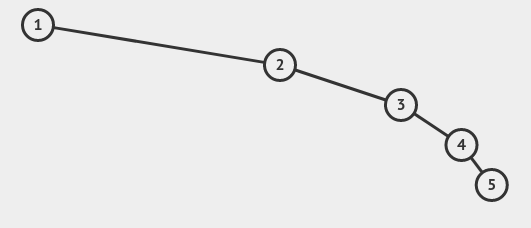
Note que a altura da árvore é 4. Se fossem adicionados $n$ elementos ordenados, a altura seria $n - 1$. Do ponto de vista assintótico, para uma BST com $n$ nós, a menor altura que uma árvore binária pode ter é $\Theta(log(n))$, enquanto que a maior altura seria $\Theta(n)$. Claramente, quando adicionamos elementos ordenados (de forma crescente ou decrescente) estamos falando do pior caso.
Uma árvore com altura $\Theta(n)$ passa a ter a eficiência similar a de uma lista. Por exemplo, a busca em uma árvore com essa altura é $\Theta(n)$. Contudo, sabemos que a árvore binária de pesquisa pode nos fornecer operações $\Theta(log(n))$ se a altura dessa árvore for controlada. Portanto, para garantir a eficiência dos algoritmos é preciso encontrar uma estratégia que mantenha a árvore com a menor altura possível. Uma dessas estratégias é discutida na seção seguinte.
A Solução: Árvores Balanceadas (AVL)
A solução para resolver o problema apresentado anteriormente é mantermos a árvore balanceada. Uma árvore pode ser considerada balanceada se a sua altura é $O(log(n))$.
A forma como o balanceamento é feito muda de acordo com o tipo da árvore. Por exemplo, as árvores AVL usam a altura de cada nó para realizar as operações de balanceamento. Já as árvores rubro-negras adicionam propriedades (cores) aos nós e alguns requisitos para mantê-la balanceada. Contudo, o denominador comum entre as várias estratégias para manter o balanceamento são as rotações nos nós desbalanceados. Neste documento iremos abordar árvores AVL – árvores que utilizam rotações para manter a altura $O(log(n))$.
O conceito de árvores balanceadas e algoritmos de balanceamento foram introduzidos por Adelson Velskii e Landis. Esses dois autores conceberam as árvores AVL, uma árvore BST balanceada. O conceito de árvore balanceada pode ser definido da seguinte maneira:
Uma árvore $<E,raiz,D>$ é balanceada se $|h(E) - h(D)| \le 1$ e se E e D são balanceadas.
Ou seja, as alturas das duas sub-árvores a partir de cada nó diferem no máximo em uma unidade. Dessa maneira, é possível garantir que as operações básicas sejam efetuadas em $O(log(n))$.
Exemplos de árvores AVL e não-AVL
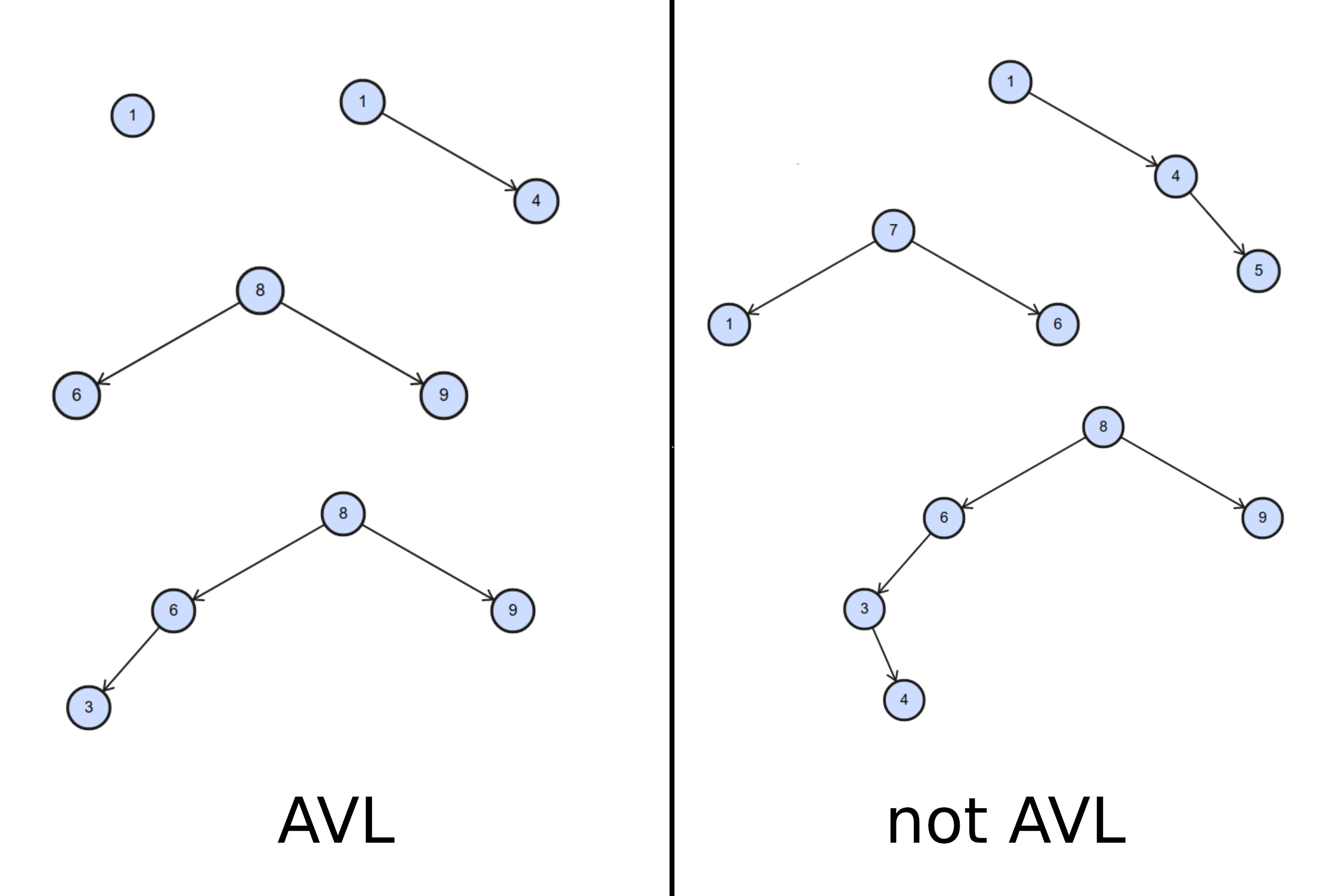
Provando que $h = O(log(n))$
Número mínimo de nós que em uma AVL de altura h. O pior caso é quando, para cada nó, a sub-árvore à direita tem altura uma unidade maior ou menor do que a sub-árvore à esquerda.
- Relação de recorrência: $N(h) = N(h-1) + N(h-2) + 1$
Essa relação é muito semelhante à relação de recorrência da função de Fibonacci. Sua resolução revela uma função exponencial. Como queremos saber o inverso (a altura), temos que $H = O (log(n))$. Mais especificamente, $H = 1.44 \log(N)$.
Como manter a árvore balanceada?
Rotações
Rotações são operações estruturais que executam em tempo constante para BSTs que, através da manipulação de referências, visam balancear uma árvore, mantendo sua propriedade de pesquisa. Rotações são realizadas após operações que quebrem a propriedade de balanceamento. Existem 4 cenários em árvores AVL que demandam rotações. Iremos explorar esses cenários após introduzir os conceitos de altura e balance de um nó.
Conceito de altura de um nó
Até aqui, estávamos trabalhando com o conceito de altura de uma árvore que, por sinal, é a altura do nó raiz. Como precisamos manter o balanceamento para todos os nós, precisamos também adicionar ao nó a informação relativa a sua altura. Portanto, há uma modificação na implementação de um No, que passa agora a registrar também a sua altura. Vejamos:
public class Node {
private int value;
private int height;
private Node left;
private Node right;
private Node parent;
...}
O cálculo da altura de um nó pode ser feito de maneira recursiva:
public int height(Node node) {
if (node == null)
return -1;
else return 1 + max(height(node.left), height(node.right))
}
Uma alternativa é não passar o nó como parâmetro na recursão. Note que os algoritmos ficam um pouco mais verborrágicos, pois precisamos checar referências nulas antes de chamar recursivamente.
public int height() {
if (this.left == null && this.right == null) return 0;
else if (this.left == null) {
return 1 + this.right.height();
} else if (this.right == null) {
return 1 + this.left.height();
} else {
return 1 + max(this.left.height(), this.right.height());
}
}
Balance de um nó
Sabendo que podemos calcular a altura da sub-árvore a esquerda e da sub-árvore à direita, podemos saber o balance de um nó. Balance é a diferença entre a altura da sub-árvore à esquerda e a altura da sub-árvore à direita.
private int balance(Node node) {
if (node != null) return height(node.left) - height(node.right);
return 0;
}
// alternativa sem passar o nó como parâmetro para recursão
private int balance() {
int left = this.left == null ? -1 : this.left.height();
int right = this.right == null ? -1 : this.right.height();
return left - right;
}
Essa informação é importante por dois motivos:
- Para sabermos se o nó respeita a restrição de AVL
- Para sabermos se o nó está “pendendo” para a esquerda ou se está “pendendo” para a direita
Note que há diferença entre desbalanceado e “pendendo” para a direita ou “pendendo” para a esquerda. Desbalanceado significa que o nó não é raiz de uma árvore AVL e, por isso, demanda o uso de rotações para tornar a árvore AVL normalmente. Os outros casos (pendendo para a direita e pendendo para a esquerda) não demandam rotações, pois ainda estão respeitando a invariante $|He - Hd| \le 1$.
Veja os exemplos a seguir. Cada nó tem um balance. Para os nós de balance -1 e 1, o sinal indica se o nó está pendendo para a direita ou para a esquerda. Se o sinal for positivo (+1), está pendendo para a esquerda. Se for negativo (-1), está pendendo para a direita. É importante reforçar que nós pendendo para a direita e para a esquerda são considerados balanceados, pois respeitam a restrição do balanceamento de uma AVL ($|balance| <= 1$). No entanto, eles estão na iminência de quebrar a restrição do balanceamento. Nós com balance 2 ou -2 estão desbalanceados.
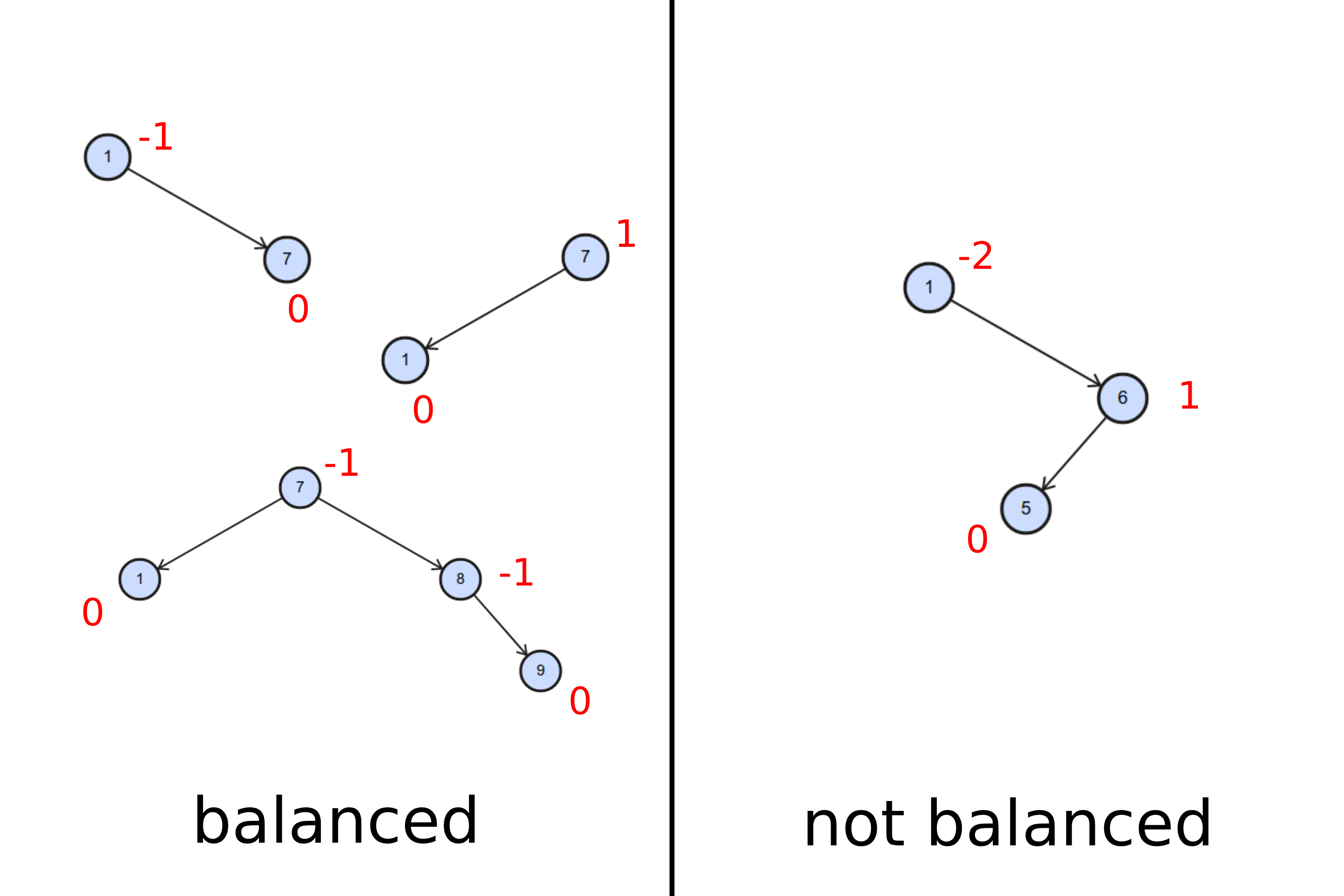
Portanto, as regras para saber se um nó está pendendo para a direita, esquerda, se está nivelado ou desbalanceado são:
- se height(node.left) - height(node.right) == 1 -> Pendendo para a esquerda
- se height(node.left) - height(node.right) == -1 -> Pendendo para a direita
- se height(node.left) - height(node.right) == 0 -> nivelado
- se |height(node.left) - height(node.right)| == 2 -> desbalanceado
Desafio. Implemente os métodos a seguir:
public boolean isLeftPending()
public boolean isRightPending()
public boolean isBalanced()
Por que precisamos saber se o nó está pendendo para a direita, esquerda, nivelado ou desbalanceado?
Porque, após inserir ou remover um elemento em uma árvore AVL, nossos algoritmos baseiam-se nessa informação para decidir se haverá rotação ou não e para onde será feita essa rotação.
Inserção em árvores AVL
A inserção em árvores AVL reutiliza a inserção de BST. No entanto, após a inserção do novo nó, precisamos atualizar as alturas de cada nó e checar se a árvore ainda é AVL. Caso não seja, precisamos aplicar as rotações necessárias.
A partir de agora, vamos abordar cada caso da inserção. Vamos adotar a seguinte nomenclatura:
- z: nó que acabou de ser adicionado
- y: pai do nó adicionado
- x: pai do pai (avô) do nó adicionado
Para fins de simplificação dos algoritmos, também vamos assumir que y e x não são nós nulos.
Caso 1. Rotação à direita: O nó foi inserido à esquerda do pai. Além disso, o pai do nó inserido é filho à esquerda de um nó pendendo para a esquerda. O código para detectar esse cenário é o seguinte:
Node y = z.parent
Node x = y.parent
if (x.isLeftPending() && y.left == z)
rotateRight(x)
Neste caso, basta aplicarmos uma rotação à direita no avô do nó inserido. Note que deve-atualizar a esquerda de x para que receba os valores à direita de y. Veja:
Material extra: esse vídeo e esse são bem interessantes.
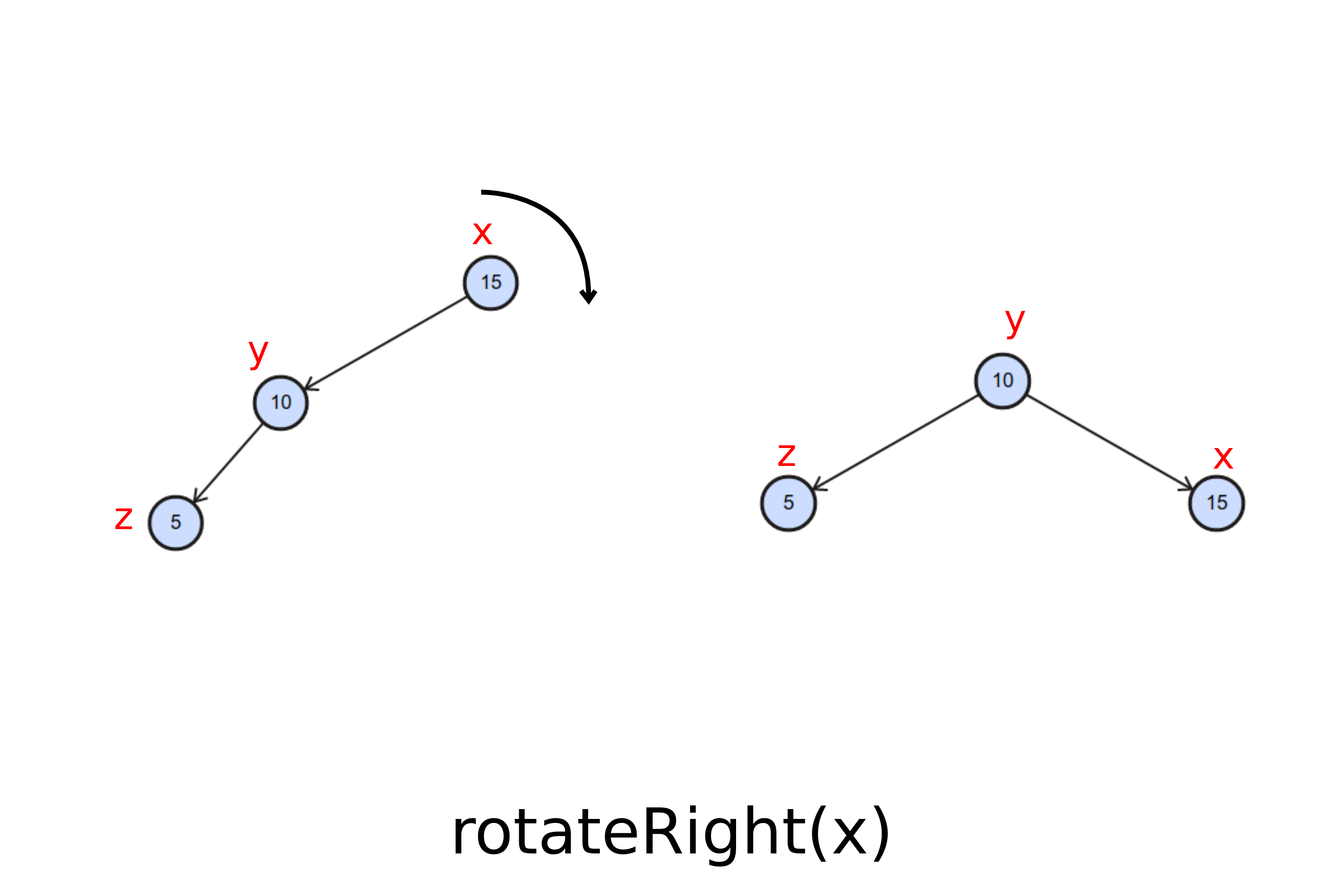
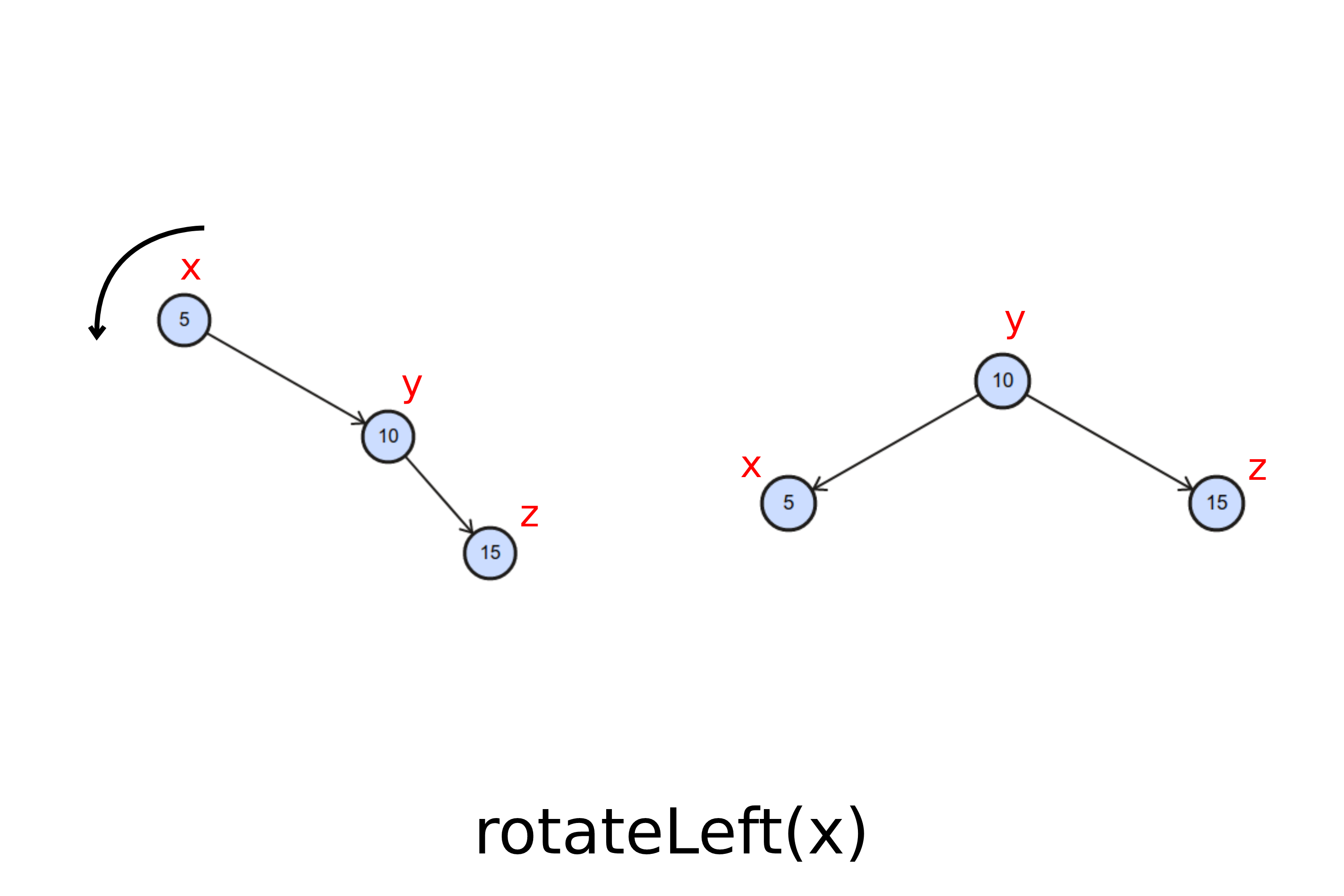
Caso 2. Rotação à esquerda: O nó foi inserido à direita do pai. Além disso, o pai do nó inserido é filho à direita de um nó pendendo para a direita.
O código para detectar esse cenário é o seguinte. Note que deve-atualizar a direita de x para que receba os valores à esquerda de y. Veja:
Node y = z.parent
Node x = y.parent
if (x.isRightPending() && y.right == z)
rotateLeft(x)
Neste caso, basta aplicarmos uma rotação à esquerda no avô do nó inserido. Veja:
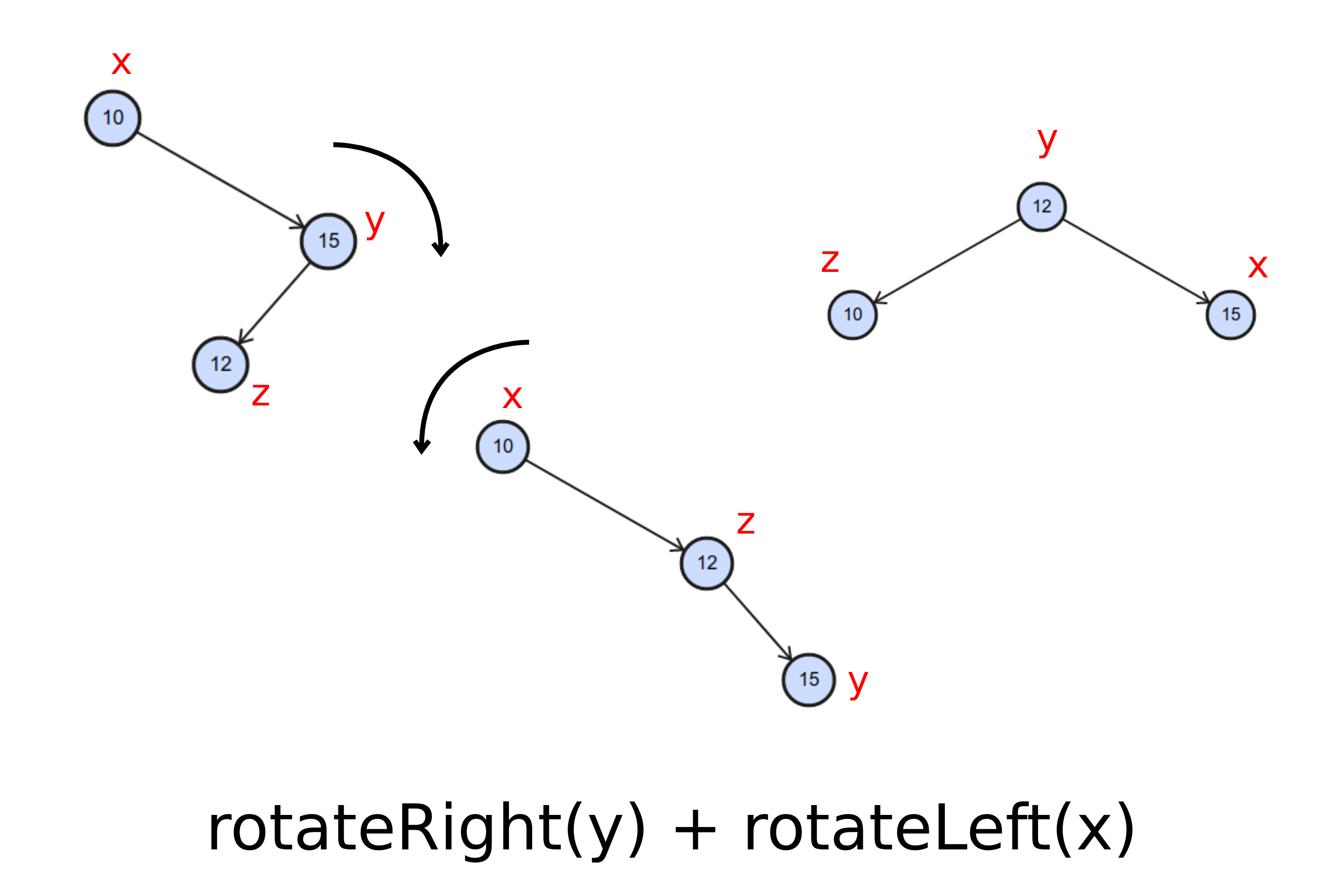
Caso 3. Rotação à direita seguida de rotação à esquerda: O nó foi inserido à esquerda do pai. Além disso, o pai do nó inserido é filho à direita de um nó pendendo para algum dos lados (cenário em Z).
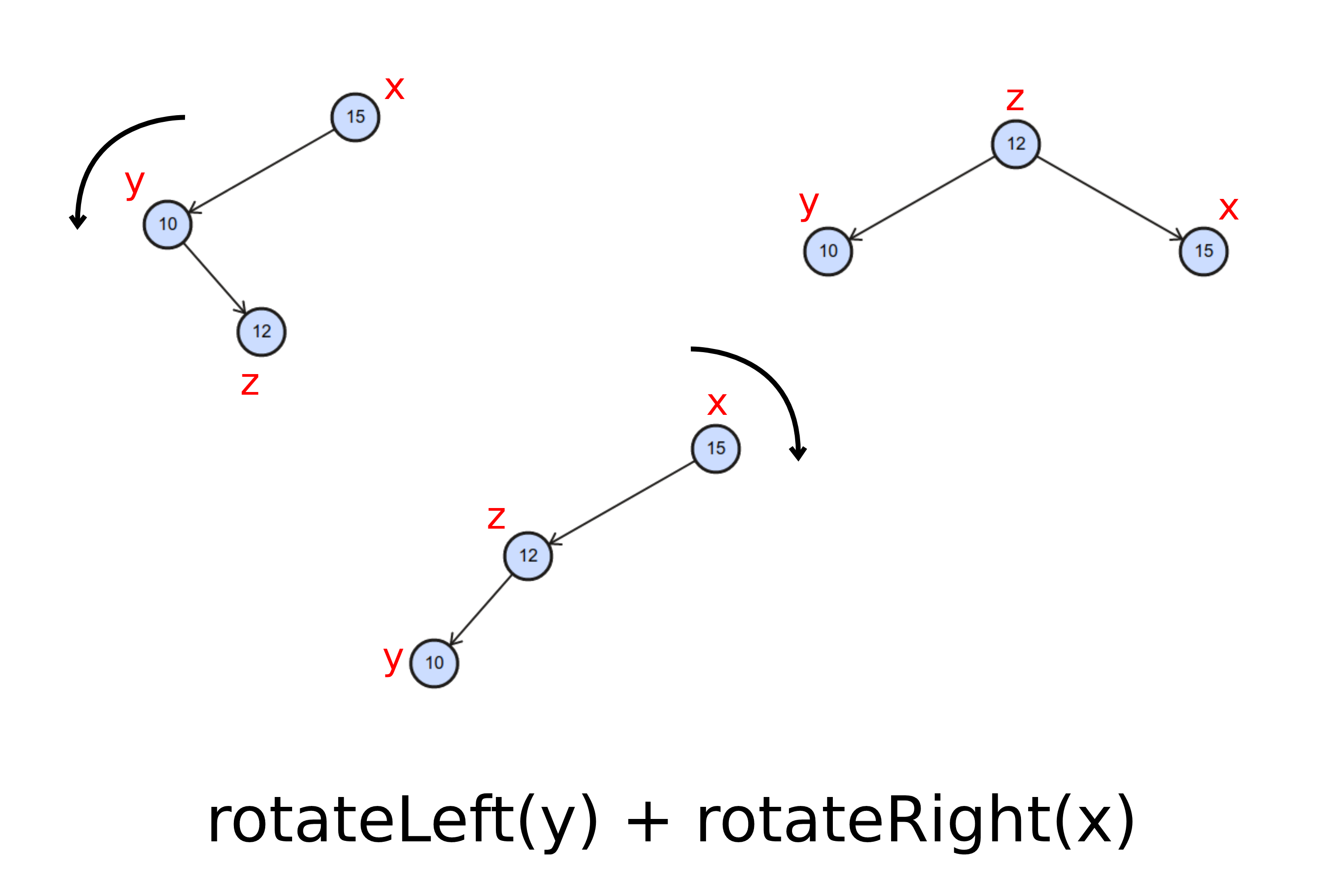
Caso 4. Rotação à esquerda seguida de rotação à direita: O nó foi inserido à direita do pai. Além disso, o pai do nó inserido é filho à esquerda de um nó pendendo para algum dos lados.
Contribuições
Pedro Serey contribuiu para a escrita deste post.